The church of Longuelo is the last main building designed by Pino Pizzigoni and could be considered his most innovative work, representing the sum of experimentation about shells made during the last twenty years of his activity. His final project was presented in May 1961. The construction started in 1962 and proceeded until 1965. The church was finally consecrated in June 1966.

For further details regarding Pino Pizzigoni and the church of Longuelo, please refer to:

DEREGIBUS C., PUGNALE A., The church of Longuelo by Pino Pizzigoni. Design and construction of an experimental structure, in “Construction History”, Vol. 25, 2010.

DEREGIBUS C., PUGNALE A., The church of Longuelo designed by Pino Pizzigoni. An unknown example of outstanding structure, Proceedings of the IASS Symposium “Evolution and trends in design, analysis and construction of shell and spatial structures”, Valencia (Spain), 28 September – 2 October 2009, pp. 1599-1610.

In this post, I am going to define in parametric terms the geometry of the church in order to run an optimization process with Grasshopper, Karamba and Galapagos.

Geometry of the church

Even though the building is geometrically complex, the concept behind its shape definition is simple and rational. The church spans over 900 square meters, with a maximum height of 18 meters – it is divided in four identical free parts which form a perfectly symmetric, centrical layout for the church.

The church is composed of four identical and symmetrical parts, connected and divided by two joints. Each of these four parts is then composed of five different shells. In order to better understand their spatial articulation, it could be helpful to begin with only considering four of these surfaces: joined together like they were shaped in a ring, that is then topologically transformed in a Möbius Ring. Moving four nodes, a whole deformation of the surfaces is added obtaining four hypars. A fifth hypar, partially capping the hole between the first four shells, is then added. These four hypars do not define a closed shape: even when the four identical parts are joined together, some holes need to be capped. For this reason, the remaining hole is finally closed with a moderate and unpretentious stained-glass window, which softly lights inner space with reflected light.

If we then move from the shells on to the bars, we can identify 14 bars creating the main frame of the structure. There are then 4 more free bars, which are not shell edges, and three foundation bars gathered in the building in a single crossbeam of generous dimensions.

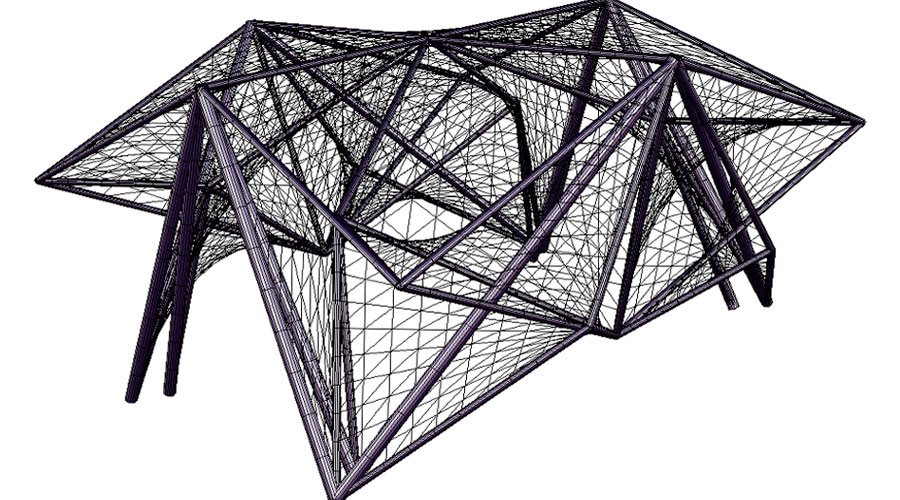
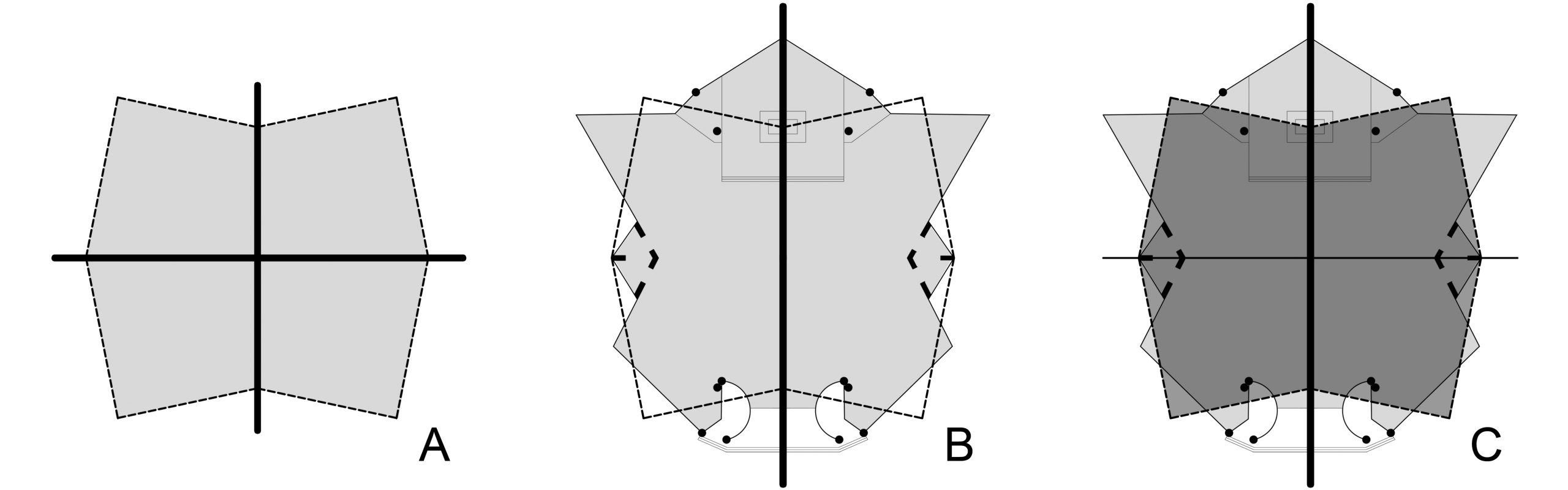
As previously described, this complicated spatial configuration only defines a quarter of the whole church building, which is simply obtained by means of two axial symmetries. The sum of these four parts becomes a roof structure composed by 20 vaults and 84 bars, connected with each other and thus giving a high sense of spatial complexity.

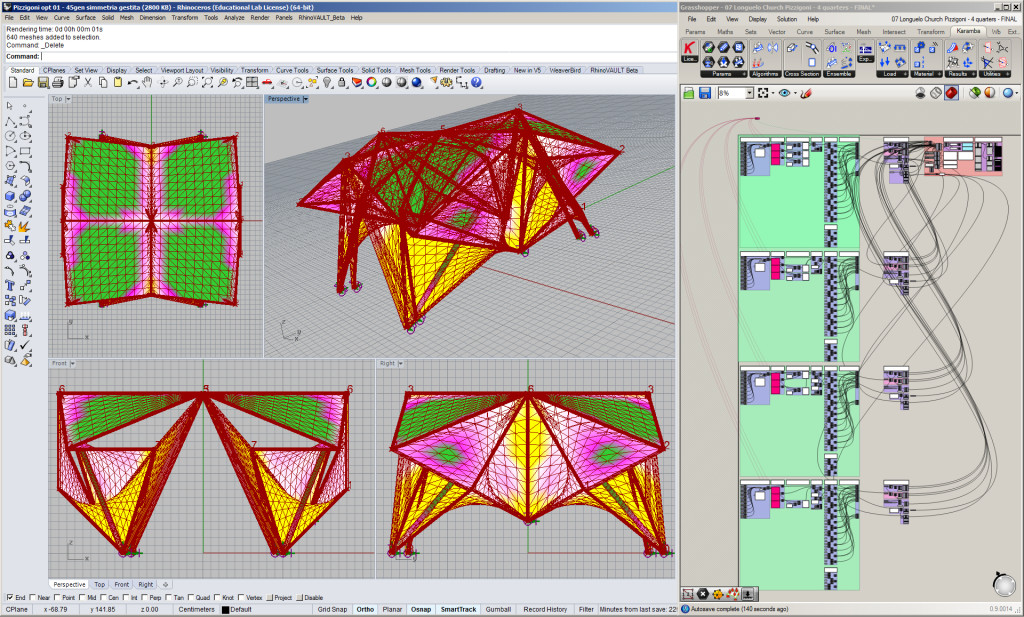
Grasshopper definition

In Grasshopper, the church has been modelled entirely in order to allow the Galapagos GA to find non-symmetric suitable configurations. Bars and shells are defined starting from 8 points for each quarter. The X,Y,Z coordinates of the original church have been used. Then, a gene pool component has been added in order to allow spatial variations and therefore optimize the overall structural behaviour. Two different files of this GH definition can be downloaded here.

One file is preserving the church symmetry locking the X and/or Y translations of some specific nodes. However, both files do not allow the supports to move on the Z axis.

The thickness of the shells has been considered 10cm, while the thickness of the bars is varying according to the survey we made (Carlo Deregibus and I) on the original project. The building is made of bars with a variable diameter (from 30 to 80 cm). In this model just two sizes have been used, 35cm and 70cm. The material defined is concrete C40/50, which is the most similar to the original one used for the construction.

The loads considered are: gravity load, self-weight and an extra distributed load of 6KN/m2 (applied as a mesh load with Karamba).

The elastic energy is used as the fitness function for the structural optimization. The original structure already presents an acceptable value for this parameter, as well as for the maximum displacement.

It is important to underline that Pizzigoni used a very different approach to conceive and calculate its structure. His work was based on a great intuition and conceptual simplification. In fact, he considered a statically-determinate frame, to which he added the self-weight of the shells. That was very far from being the proper simulation of the real condition. However, any effort spent to reconstruct the process followed by Pizzigoni is destined to fail as all the corrections can only be hypothesized. Probably, the absence of comprehensive normative rules gave designers, with a certain amount of irresponsibility, a general sense of freedom in defining their structures only on the basis of their own instinct, and this is why the result is so extraordinary. A similar complex covering is surely an exceptional example of that “structural intuition”, which nowadays seems so rare and which was so useful in managing situations characterized by high degrees of uncertainty.

Structural optimisation

Running a structural optimisation of this church is very time consuming (especially using a Genetic Algorithm). The process works for several hours and sometimes needs to be stopped and guided by the user. Galapagos either converges too fast towards sub-optimal solutions or does not converge at all. A test with Goat would surely show a different scenario: gradient-based algorithm are generally much faster when they have to deal with this kind of problems (in which we start from a previously defined shape and we just want to optimize it). At present, Goat does not support the use of Gene pools. This means that those coordinates have to be changed with sliders. You can try yourself starting from my files.

I am not going to draw fitness graphs, as it is very difficult to extract data from Galapagos. You can try yourself to run the algorithm and explore a rich set of solutions which are found generation by generation. I personally did not run enough the algorithm to be able to express a scientific opinion. However, I am not so interested in these kinds of optimizations as finding out if the original structure is optimal or if there are better ones does not make any sense. Below you can find a screenshot of the process.

Computational Morphogenesis

Even though I personally do not see any advantage in optimizing an existing structure (I would not know how to compare the results with the original design, since that was conceived in a completely different way and a comparison does not make sense), the church of Longuelo is an excellent example to try out a real computational process of morphogenesis. On the contrary, comparing the two design approaches does make sense (especially to emphasize the design potential of the tools we have got now). A process based on intuition, experience and conceptual simplification to reach structural complexity is worth to be compared to the digital method: parametric definition of boundary conditions and design variables, fitness function and a GA as the search tool. The 8 points defining bars and shells can be used as the reference to automatically generate 14 bars and, as a consequence, 5 shells using some of them as edges. A penalty function would control self-intersections and Karamba would evaluate the structural behaviour of the configurations generated. Spatial complexity would be now handled with a parametric model able to generate different topological configurations of the church and a meta-heuristic optimization algorithm.

I have already worked on this file, but it is very difficult to organize the fitness and penalty functions in order to allow the GA to explore a wide set of possibilities. I am still thinking about this problem, which is mainly a design problem and not just a matter of technical implementation. I wish I can post some results soon. But for the moment, I am proposing a usual optimization with numerical tools of an existing old building.